Les Types Abstraits de Données : listes, files, piles…

• Fonctions et procédures II : la récursivité
• Sommaire
• [TP] Le jeu du serpent

Dans ce chapitre, nous allons aborder un nouveau type composite : les Types Abstraits de Données, aussi appelés TAD. De quoi s'agit-il ? Eh bien pour le comprendre, il faut partir du problème qui amène à leur création. Nous avons vu au début de la partie III le type ARRAY. Les tableaux sont très pratiques mais ont un énorme inconvénient : il sont contraints. Leur taille est fixée au début du programme et ne peut plus bouger. Imaginons que nous réalisions un jeu d'aventure. Notre personnage découvre des trésors au fil de sa quête, qu'il ajoute à son coffre à trésor. Ce serait idiot de créer un objet coffre de type Tableau. S'il est prévu pour contenir 100 items et que l'on en découvre 101, il sera impossible d'enregistrer notre 101ème item dans le coffre ! Il serait judicieux que le coffre puisse contenir autant de trésors qu'on le souhaite.

Eh bien non, pas tout à fait. Nous allons donc devoir en créer nous mêmes, avec nos petits doigts : des «listes» d'éléments possiblement infinies. C'est ce que l'on appelle les TAD. Nous ferons un petit tour d'horizon théorique de ce que sont les Types Abstraits de Données. Puis nous créerons dans les parties suivantes quelques types abstraits avant de voir ce que le language Ada nous propose. Nous créerons également les outils minimums nécessaires à leur manipulation avant de voir un exemple d'utilisation.

• Qu'est-ce qu'un Type Abstrait de Données ?
• Les piles
• Les files
• Les listes chaînées

Qu'est-ce qu'un Type Abstrait de Données ?

Un premier cas

Comme je viens de vous le dire, les Types Abstraits de Données peuvent s'imaginer comme des «listes» d'éléments. Les tableaux constituent un type possible de TAD. Mais ce qui nous intéresserait davantage, ce serait des «listes infinies». Commençons par faire un point sur le vocabulaire employé. Lorsque je parle de «liste», je commets un abus de langage. En effet, il existe plusieurs types abstraits, et les listes (je devrais parler plus exactement de "listes chaînées" par distinction avec les tableaux) ne constituent qu'un type abstrait parmi tant d'autres. Mais pour mieux comprendre ce que peut être un TAD, nous allons pour l'instant nous accommoder de cet abus (je mettrai donc le mot liste entre guillemets). Voici une représentation possible d'un Type Abstrait de Donnée :

• «Liste» vide : un emplacement mémoire a été réquisitionné pour la liste, mais il ne contient rien.

• «Liste» contenant un élément : le premier emplacement mémoire contient un nombre (ici 125) et pointe sur un second emplacement mémoire, encore vide pour l'instant.

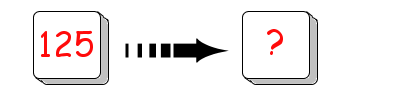
• «Liste» contenant 3 éléments : trois emplacements mémoires ont été réquisitionnés pour contenir des nombres qui se sont ajoutés les uns à la suite des autres. Chaque emplacement pointe ainsi sur le suivant. Le troisième pointe quant à lui sur un quatrième emplacement mémoire vide.

Autres cas

L'exemple ci-dessus est particulier, à plusieurs égards. Il n'existe pas qu'un seul type de «liste» (et je ne compte pas les traiter toutes). La «liste» vue précédemment dispose de certaines propriétés qu'il nous est possible de modifier pour en élaborer d'autres types.

Contraintes de longueur

La «liste» vue ci-dessus n'a pas de contrainte de longueur. On peut y ajouter autant d'éléments que la mémoire de l'ordinateur peut en contenir mais il est impossible d'obtenir le 25ème élément directement, il faut pour cela la parcourir à partir du début. Les tableaux sont quant à eux des listes contraintes et indexées de manière à accéder directement à tout élément, mais la taille est donc définie dès le départ et ne peut plus être modifiée par la suite. Mais vous aurez compris que dans ce chapitre, les tableaux et leurs contraintes de longueur ne nous intéressent guère.

Chaînage

Chaque élément pointe sur son successeur. On dit que la «liste» est simplement chaînée. Une variante serait que chaque élément pointe également sur son prédécesseur. On dit alors que la «liste» est doublement chaînée.

Linéarité

Chaque élément ne pointe que sur un seul autre élément. Il est possible de diversifier cela en permettant à chaque élément de pointer sur plusieurs autres (que ce soit un nombre fixe ou illimité d'éléments). On parlera alors d'arbre et non plus de «liste».

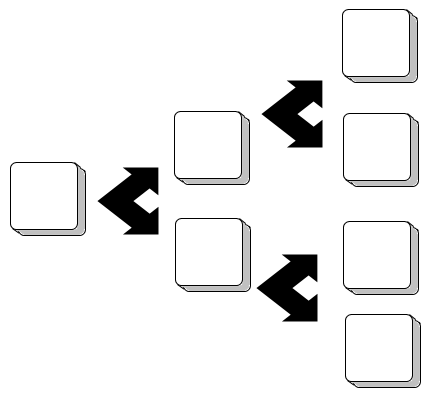
Méthode d'ajout

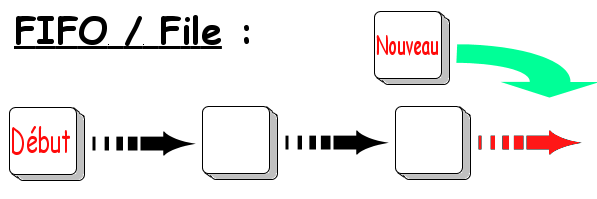
Chaque élément ajouté l'a été en fin de «liste». Cette méthode est dite FIFO pour First In/First Out, c'est-à-dire «premier arrivé, premier servi». Le second élément ajouté sera donc en deuxième position, le troisième élément en troisième position… notre «liste» est ce que l'on appelle une file (en Français dans le texte). C'est ce qui se passe avec les imprimantes reliées à plusieurs PC : le premier à appuyer sur "Impression" aura la priorité sur tous les autres. Logique, me direz-vous.

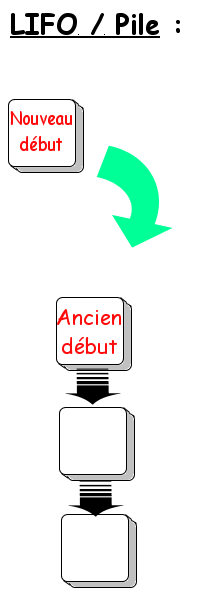
Mais ce n'est pas obligatoirement le cas. La méthode «inverse» est dite LIFO pour «Last In/First Out», c'est-à-dire «dernier arrivé, premier servi». Le premier élément ajouté sera évidemment le premier de la «liste». Lorsque l'on ajoute un second élément, c'est lui qui devient le premier de la «liste» et l'ex-premier devient le second. Si on ajoute un troisième élément, il sera le premier de la «liste», l'ex-premier devient le second, l'ex-second (l'ex-ex-premier) devient le troisième… on dira alors que notre «liste» est une pile. On peut se représenter la situation comme une pile d'assiette : la dernière que vous ajoutez devient la première de la pile. L'historique de navigation de votre navigateur internet agit tel une pile : lorsque vous cliquez sur précédent, la première page qui s'affichera sera la dernière à laquelle vous aviez accédé. La «liste» des modifications apportées à un document est également gérée telle une pile : cliquez sur Annuler et vous annulerez la dernière modification.

Cyclicité

Le dernier élément de notre liste ne pointe sur rien du tout ! Or nous pourrions faire en sorte qu'il pointe sur le premier élément. Il n'y a alors ni début, ni fin : notre liste est ce que l'on appelle un cycle.

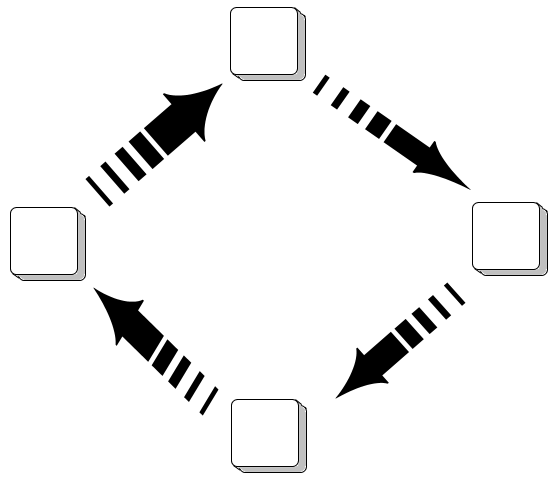
Il est bien sûr possible de combiner différentes propriétés : arbres partiellement cycliques, cycles doublement chaînés… pour élaborer de nouvelles structures.

Primitives

Mais un type abstrait de données se définit également par ses primitives. De quoi s'agit-il ? Les primitives sont simplement les fonctions essentielles s'appliquant à notre structure. Ainsi, pour une file, la fonction Ajouter_a_la_fin( ) constitue une primitive. Pour une pile, ce pourrait être une fonction Ajouter_sur_la_pile( ).

En revanche, une fonction Ranger_a_l_envers(p : pile ) ou Mettre_le_chantier(f : file) ou Reduire_le_nombre_de_branche(a:arbre) ne sont pas des primitives : ce ne sont pas des fonctions essentielles au fonctionnement et à l'utilisation de ces structures (même si ces fonctions ont tout à fait le droit d'exister).

Donc créer un TAD tel une pile, une file… ce n'est pas seulement créer un nouveau type d'objet, c'est également fournir les primitives qui permettront au programmeur final de le créer, de le détruire, de le manipuler… sans avoir besoin de connaître sa structure. C'est cet ensemble TAD-Primitives qui constitue ce que l'on appelle une Structure de données.

Une liste chaînée est une structure de données (c'est à dire un type abstrait de données fourni avec des primitives) linéaire et non contrainte. Elle peut être cyclique ou non, simplement ou doublement chaînée. L'accès aux données doit pouvoir se faire librement (ni en FIFO, ni en LIFO) : il doit être possible d'ajouter/modifier/retirer n'importe quel élément sans avoir préalablement retiré ceux qui le précédaient ou le suivaient. Toutefois, il faudra très souvent parcourir la liste chaînée depuis le début avant de pouvoir effectuer un ajout, une modification ou une suppression.

Pour mieux comprendre, je vous propose de créer quelques types abstraits de données (que je nommerai désormais TAD, je sais je suis un peu fainéant ). Je vous propose de construire successivement une pile puis une file avant de nous pencher sur les listes chaînées. Cela ne couvrira sûrement pas tout le champ des TAD (ce cours n'y suffirait pas) mais devrait vous en donner une bonne idée et vous livrer des outils parmi les plus utiles à tout bon programmeur.

Les piles

Nous allons tout d'abord créer un type T_Pile ainsi que les primitives associées. Pour faciliter la réutilisation de ce type composite, nous écrirons tout cela dans un package que nous appellerons P_Piles. Vous remarquerez les quelques subtilités d'écriture : P_Pile pour le package ; T_Pile pour le type ; Pile pour la variable. Ce package comportera donc le type T_Pile et les primitives. Nous ajouterons ensuite quelques procédures et fonctions utiles (mais qui ne sont pas des primitives).

Création du type T_Pile

Tout d'abord, rappelons succinctement ce que l'on entend par «pile». Une pile est un TAD linéaire, non cyclique, simplement chaîné et non contraint. Tout ajout/suppression se fait par la méthode LIFO : Last In, First Out ; c'est à dire que le programmeur final ne peut accéder qu'à l'élément placé sur le dessus de la pile. Alors, comment créer une liste infinie de valeurs liées les unes aux autres ? Nous avions dors et déjà approché cette idée lors du précédent chapitre sur les pointeurs. Il suffirait d'un pointeur pointant sur un pointeur pointant sur un pointeur pointant sur un pointeur… Mais, premier souci, où et comment enregistre-t-on nos données s'il n'y a que des pointeurs ? Une idée ? Avec un type structuré bien sûr ! Schématiquement, nous aurions ceci :

1
2
3
4

DECLARATION DE MonType :
   Valeur : integer, float ou que sais-je ; 
   Pointeur_vers_le_prochain : pointeur vers MonType ;
FIN DE DECLARATION

Nous pourrions également ajouter une troisième composante (appelée Index ou Indice) pour numéroter nos valeurs. Nous devrons également déclarer notre type de pointeur ainsi :

1

TYPE T_Pointeur IS ACCESS MonType ;

Sauf que, deuxième souci, si nous le déclarons après MonType, le compilateur va se demander à quoi correspond la composante Pointeur_vers_le_prochain. Et si nous déclarons T_Pointeur avant MonType, le compilateur ne comprendra pas vers quoi il est sensé pointé.

Comment résoudre ce dilemme ? C'est le problème de l’œuf et de la poule : qui doit apparaître en premier ? Réfléchissez. Là encore, vous connaissez la solution. Nous l'avons employée pour les packages : il suffit d'employer les spécifications ! Il suffit que nous déclarions MonType avec une spécification (pour rassurer le compilo ), puis le type T_Pointeur et enfin que nous déclarions vraiment MonType. Compris ? Alors voilà le code correspondant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

TYPE T_Cellule;                     --T_Cellule correspond à un élément de la pile

TYPE T_Pile IS ACCESS T_Cellule;   --T_Pile correspond au pointeur sur un élément

TYPE T_Cellule IS
   RECORD
      Valeur  : Integer; --Ici on va créer une pile d'entiers
      Index   : Integer; --Le dernier élément aura l'index N°1
      Suivant : T_Pile ; --Le suivant correspond à une «sous-pile»
   END RECORD;

Création des primitives

L'idée, en créant ce package, est de concevoir un type T_Pile et toutes les primitives nécessaires à son utilisation de sorte que tout programmeur utilisant ce package n'ait plus besoin de connaître la structure du type T_Pile : il doit tout pouvoir faire avec les primitives fournies sans avoir à mettre les mains dans le cambouis (Nous verrons plus tard comment lui interdire tout accès à ce «cambouis» avec la privatisation de nos packages). De quelles primitives a-t-on alors besoin ? En voici une liste avec le terme anglais généralement utilisé et une petite explication :

• Empiler (Push) : ajoute un élément sur le dessus de la pile. Cet élément devient alors le premier et son indice (composante Index) est supérieur d'une unité à «l'ex-premier» élément.
• Dépiler (Pop) : retire le premier élément de la pile, la première cellule. Cette fonction renvoie en résultat la valeur de cette cellule.
• Pile_Vide (Empty) : renvoie TRUE si la pile est vide (c'est-à-dire si pile = NULL). Primitive importante car il est impossible de dépiler une pile vide.
• Longueur (Length) : renvoie la longueur de la pile, c'est à dire le nombre de cellules qu'elle contient.
• Premier (First) : renvoie la valeur de la première cellule de la pile sans la dépiler.

Bien, il ne nous reste plus qu'à créer ces primitives. Commençons par la procédure Push(P,n). Elle va recevoir une pile P, qui n'est rien d'autre qu'un pointeur vers la cellule située sur le dessus de la pile. P sera en mode IN OUT. Elle recevra également un Integer n (puisque nous avons choisi les Integer, mais nous pourrions tout aussi bien le faire avec des float ou autre chose). Elle va devoir créer une cellule (et donc un index), la faire pointer sur la cellule située sur le dessus de la pile avant d'être elle-même pointée par P. Compris ? Alors allez-y !

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

PROCEDURE Push (P : IN OUT T_Pile; N : IN Integer) IS
   Cell : T_Cellule;
BEGIN
   Cell.Valeur := N ;
   IF P /= NULL
      THEN Cell.Index := P.All.Index + 1 ;
           Cell.Suivant := P.All'ACCESS ;
      ELSE Cell.Index := 1 ;
   END IF ;
   P := NEW T_Cellule'(Cell) ;
END Push ;

1

P:= Cell'access ;

Votre procédure Push() est créée ? Enregistrez votre package et créez un programme afin de le tester. Exemple :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

with ada.Text_IO, Ada.Integer_Text_IO, P_Pile ; 
use ada.Text_IO, Ada.Integer_Text_IO, P_Pile ; 

Procedure test is
   P : T_Pile ; 
BEGIN
   Push(P,3) ; Push(P,5) ; Push(P,1) ; Push(P,13) ; 

   Put(P.all.Index) ;                      Put(P.all.Valeur) ; new_line ; 
   Put(P.Suivant.Index) ;                  Put(P.Suivant.Valeur) ; new_line ; 
   Put(P.Suivant.suivant.Index) ;          Put(P.Suivant.suivant.Valeur) ; new_line ; 
   Put(P.suivant.suivant.suivant.Index) ;  Put(P.Suivant.Suivant.Suivant.Valeur) ; 
end Test ;

Maintenant, la procédure Pop(P,N). Je ne reviens pas sur les paramètres ou sur le sens de cette fonction, j'en ai déjà parlé. Je vous rappelle toutefois que cette procédure doit retourner, non pas un objet de type T_Cellule, mais une variable de type Integer, et «rétrécir» la pile. Les paramètres devront donc être en mode OUT (voire IN OUT). Dernier point, si la pile est vide, le programmeur qui utilisera votre package (appelons-le « programmeur final ») ne devrait pas la dépiler, mais il lui revient de le vérifier à l'aide de la primitive Empty : ce n'est pas le rôle de nos primitives de gérer les éventuelles bêtises du programmeur final. En revanche, c'est à vous de gérer le cas où la pile ne contiendrait qu'une seule valeur et deviendrait vide dans le code de votre primitive.

1
2
3
4
5
6
7
8
9

PROCEDURE pop(P : IN OUT T_Pile ; N : OUT Integer) IS
BEGIN
   N := P.all.valeur ;     --ou P.valeur
                           --P.all est censé exister, ce sera au programmeur final de le vérifier
   IF P.all.suivant /= NULL
      THEN P := P.suivant ; 
      ELSE P := null ;
   END IF ;
END Pop ;

Maintenant que vos deux procédures principales sont créées (je vous laisse le soin de les tester) nous n'avons plus que trois primitives (assez simples) à coder : Empty( ), First( ) et Length( ). Toutes trois sont des fonctions ne prenant qu'un seul paramètre : une pile P. Elles retourneront respectivement un booléen pour la première et un integer pour les deux suivantes. Je vous écris ci-dessous le code source de P_Pile.adb et P_Pile.ads. Merci qui ?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

PACKAGE BODY P_Pile IS

   PROCEDURE Push (
         P : IN OUT T_Pile;
         N : IN     Integer) IS
      Cell : T_Cellule;
   BEGIN
      Cell.Valeur := N ;
      IF P /= NULL
            THEN
         Cell.Index := P.All.Index + 1 ;
         Cell.Suivant := P.All'ACCESS ;
      ELSE
         Cell.Index := 1 ;
      END IF ;
      P := NEW T_Cellule'(Cell) ;
   END Push ;


   PROCEDURE Pop (
         P : IN OUT T_Pile;
         N :    OUT Integer) IS
   BEGIN
      N := P.All.Valeur ;     --ou P.valeur
      --P.all est censé exister, ce sera au programmeur final de le vérifier
      IF P.All.Suivant /= NULL
            THEN
         P := P.Suivant ;
      ELSE
         P := NULL ;
      END IF ;
   END Pop ;

   FUNCTION Empty (
         P : IN     T_Pile)
     RETURN Boolean IS
   BEGIN
      IF P=NULL
            THEN
         RETURN True ;
      ELSE
         RETURN False ;
      END IF ;
   END Empty ;

   FUNCTION Length(P : T_Pile) RETURN Integer IS
   BEGIN
      IF P = NULL 
         THEN RETURN 0 ; 
      ELSE RETURN P.Index ; 
      END IF ; 
   END Length ; 
   
   FUNCTION First(P : T_Pile) RETURN Integer IS 
   BEGIN
      RETURN P.Valeur ; 
   END First ; 

END P_Pile;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

PACKAGE P_Pile IS
   
   TYPE T_Cellule;                  --T_Cellule correspondant à un élément de la pile

   TYPE T_Pile IS ACCESS ALL T_Cellule;--T_Pile correspondant au pointeur sur un élément

   TYPE T_Cellule IS
      RECORD
         Valeur  : Integer; --On crée une pile d'entiers
         Index   : Integer;
         Suivant : T_Pile;  --Le suivant correspond à une "sous-pile"
      END RECORD;

   PROCEDURE Push (P : IN OUT T_Pile; N : IN Integer) ;

   PROCEDURE Pop (P : IN OUT T_Pile ; N : OUT Integer) ;

   FUNCTION Empty (P : IN T_Pile) RETURN Boolean ;
      
   FUNCTION Length(P : T_Pile) RETURN Integer ;   
   FUNCTION First(P : T_Pile) RETURN Integer ;
END P_Pile;

Jouons avec le package P_Pile

Notre package est enfin fini. Notre TAD est prêt à l'emploi et j'impose maintenant une règle : interdiction de manipuler nos piles autrement qu'à l'aide de nos 5 primitives ! Donc, plus de P.valeur, seulement des First(P) ! Plus de P.suivant, il faudra faire avec Pop(P) ! Cela va quelque peu compliquer les choses mais nous permettra de comprendre comment se manipulent les TAD sans pour autant partir dans des programmes de 300 lignes. L'objectif avec notre type T_Pile, sera de créer une procédure Put(p : T_Pile) qui se charge d'afficher une pile sous forme de colonne. Attention, le but de ce cours n'est pas de créer toutes les fonctions ou procédures utiles à tous les TAD. Il serait par exemple intéressant de créer une procédure ou une fonction get(P). Mais nous n'allons nous concentrer que sur une seule procédure à chaque fois. Libre à vous de combler les manques.

Concernant notre procédure Put(P), deux possibilités s'offrent à nous : soit nous employons une boucle itérative (LOOP, FOR, WHILE), soit nous employons une boucle récursive. Vous allez vous rendre compte que la récursivité sied parfaitement aux TAD (ce sera donc ma première solution), mais je vous proposerai également deux autres façons de procéder (avec une boucle FOR et une boucle WHILE). Voici le premier code, avec la méthode récursive :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

procedure Put(P : T_Pile) is
   Pile : T_Pile := P ; 
   N : integer ; 
begin
   if not Empty(Pile)
      then pop(Pile, N) ; 
           Put(N) ; 
           new_line ; 
           Put(Pile) ; 
   end if ; 
end Put ;

Regardons un peu ce code. Tout d'abord, c'est un code que j'aurais tout à fait pu vous proposer avant le chapitre sur les pointeurs : qui peut deviner en voyant ces lignes comment est constitué le type T_Pile ? Personne, car nous avons fourni tous les moyens pour ne pas avoir besoin de le savoir (c'est ce que l'on appelle l'encapsulation, encore une notion que nous verrons dans la partie IV). Que fait donc ce code ? Tout d'abord il teste si la pile est vide ou non. Ce sera toujours le cas. Si elle est vide, c'est fini ; sinon, on dépile la pile afin de pouvoir afficher son premier élément puis on demande d'afficher la nouvelle pile, privée de sa première cellule. J'aurais pu également écrire Put(First(Pile)) avant de dépiler, mais cela m'aurait contraint à manipuler deux fois la pile sans pour autant économiser de variable.

Non ! Surtout pas ! Tout d'abord, je vous rappelle que P est obligatoirement en mode IN puisqu'il est transmis à la fonction Empty(). Or, la procédure pop( ) a besoin d'un paramètre en mode OUT pour pouvoir dépiler. Il y aurait un conflit. Ensuite, en supposant que le compilateur ne bronche pas, que deviendrait P après son affichage ? Eh bien P serait vide, on aurait perdu toutes les valeurs qui la composait, simplement pour un affichage. C'est pourquoi j'ai créé un objet Pile qui sert ainsi de «roue de secours». Voici maintenant une solution itérative :

1
2
3
4
5

while not Empty(Pile) loop
   put(First(P)) ; 
   pop(Pile, N) ; 
   new_line ; 
end loop ;

On répète ainsi les opérations tant que la liste n'est pas vide : afficher le premier élément, dépiler. Enfin, voici une seconde solution itérative (dernière solution proposée) :

1
2
3
4
5

for i in 1..Length(P) loop
   put(first(Pile)) ; 
   pop(Pile,N) ; 
   new_line ; 
end loop ;

Ce qui est utilisé ici, ce n'est pas le fait que la liste soit vide, mais le fait que sa longueur soit nulle. Les opérations sont toutefois toujours les mêmes.

Les files

Implémentation

Deuxième exemple, les files. Nous allons donc créer un nouveau package P_File. La différence avec la pile ne se fait pas au niveau de l'implémentation. Les files restent linéaires, non cycliques, simplement chaînées et non contraintes.

1
2
3
4
5
6
7
8

TYPE T_Cellule;
TYPE T_File IS ACCESS ALL T_Cellule;
TYPE T_Cellule IS
   RECORD
      Valeur  : Integer; 
      Index   : Integer;
      Suivant : T_File; 
   END RECORD;

La différence se fait donc au niveau des primitives puisque c'est la «méthode d'ajout» qui diffère. Les files sont gérées en FIFO : first in, first out. Imaginez pour cela une file d'attente à une caisse : tout nouveau client (une cellule) doit se placer à la fin de la file, la caissière (le programmeur final ou le programme) ne peut traiter que le client en début de file, les autres devant attendre leur tour. Alors de quelles primitives a-t-on besoin ?

• Enfiler (Enqueue) : ajoute un élément à la fin de la file. Son indice est donc supérieur d'une unité à l'ancien dernier élément.
• Défiler (Dequeue) : renvoie le premier élément de la file et le retire. Cela implique de renuméroter toute la file.
• File_Vide (Empty) ; Longueur (Length) ; Premier (First) : même sens et même signification que pour les piles.

Notre travail consistera donc à modifier notre package P_Pile en conséquence. Attention à ne pas aller trop vite ! Les changements, même s'ils semblent a priori mineurs, ne portent pas seulement sur les noms des primitives. L'ajout d'une cellule notamment, n'est plus aussi simple qu'auparavant. Ce travail étant relativement simple (pour peu que vous le preniez au sérieux), il est impératif que vous le fassiez par vous-même ! Cela constituera un excellent exercice sur les pointeurs et la récursivité. Ne consultez mon code qu'à titre de correction. C'est important avant d'attaquer des TAD plus complexes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

PACKAGE BODY P_File IS

   PROCEDURE Enqueue (F : IN OUT T_File ; N : IN     Integer) IS
      Cell : T_Cellule;
   BEGIN
      Cell.Valeur := N ;
      Cell.Suivant := NULL ;
      IF F = NULL                                 --Cas où la liste est vide
            THEN Cell.Index := 1 ;
                 F := NEW T_Cellule'(Cell) ;
      ELSIF F.Suivant = NULL                      --Cas où l'on se "situe" sur le dernier élément
            THEN Cell.Index := F.Index + 1 ;
                 F.Suivant := NEW T_Cellule'(Cell) ;
            ELSE Enqueue(F.Suivant, N) ;          --Cas où l'on n'est toujours pas à la fin de la file
      END IF ;
   END Enqueue;


   PROCEDURE Dequeue (F : IN OUT T_File ; N :    OUT Integer) IS
      
      procedure Decrement(F : IN T_File) is
      begin
         if F /= null
            then F.index := F.index - 1 ;
                 Decrement(F.suivant) ; 
         end if ; 
      end Decrement ; 
      
   BEGIN
      N := F.Valeur ;               --F.all est censé exister, ce sera au Programmeur final de le vérifier.
      IF F.Suivant /= NULL
            THEN decrement(F) ;     -- !!! Il faut décrémenter les indices !!!
                 F := F.Suivant ;
            ELSE F := NULL ;
      END IF ;
   END Dequeue;

   FUNCTION Empty (F : IN     T_File) RETURN Boolean IS
   BEGIN
      IF F=NULL
            THEN RETURN True ;
            ELSE RETURN False ;
      END IF ;
   END Empty ;

   FUNCTION Length (F : T_File) RETURN Integer IS
   BEGIN
      IF F = NULL
            THEN RETURN 0 ;
      ELSIF F.Suivant = NULL
            THEN RETURN F.Index ;
            ELSE RETURN Length(F.Suivant) ;
      END IF ;
   END Length ;

   FUNCTION First ( F : T_File) RETURN Integer IS
   BEGIN
      RETURN F.Valeur ;
   END First ;

END P_File;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

PACKAGE P_Pile IS

   TYPE T_Cellule;                  --T_Cellule correspondant à un élément de la pile

   TYPE T_Pile IS ACCESS ALL T_Cellule;--T_Pile correspondant au pointeur sur un élément

   TYPE T_Cellule IS
      RECORD
         Valeur  : Integer; --On crée une pile d'entiers
         Index   : Integer;
         Suivant : T_Pile;  --Le suivant correspond à une "sous-pile"
      END RECORD;

   PROCEDURE Push (P : IN OUT T_Pile; N : IN Integer) ;
   PROCEDURE Pop (P : IN OUT T_Pile ; N : OUT Integer) ;
   FUNCTION Empty (P : IN T_Pile) RETURN Boolean ;
   FUNCTION Length(P : T_Pile) RETURN Integer ;
   FUNCTION First(P : T_Pile) RETURN Integer ;
END P_Pile;

Amusons-nous encore

Comme promis, nous allons désormais tester notre structure de données. Mais hors de question de se limiter à refaire une procédure Put( ) ! Ce serait trop simple. Cette fois nous allons également créer une fonction de concaténation !

Pas d'emballement ! La concaténation est une chose toute simple ! Cela consiste juste à mettre bout à bout deux listes pour en faire une plus grande ! Le symbole régulièrement utilisé en Ada (et dans de nombreux langages) est le symbole & (le ET commercial, aussi appelé esperluette). Vous vous souvenez ? Nous l'avions vu lors du chapitre sur les chaînes de caractère. Donc à vous de créer cette fonction de sorte que l'on puisse écrire : File1 := File2 & File 3 ! N'oubliez pas auparavant de créer une procédure put( ) pour contrôler vos résultats et prenez garde que l'affichage d'une file ne la défile pas définitivement !

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

procedure Put(F : in out T_File) is
   N : integer ; 
begin
   for i in 1..length(F) loop
      dequeue(F,N) ; 
      put(N) ; 
      enqueue(F,N) ;       --on n'oublie pas de réenfiler l'élement N pour ne pas vider notre file !
   end loop ; 
end Put ; 

function"&"(left,right : in T_File) return T_File is
   N : integer ;
   L : T_File := Left ; 
   R : T_File := Right ; 
   res : T_File ; 
begin
   for i in 1..length(left) loop    --on place les éléments de la file de gauche dans la file résultat
      dequeue(L,N) ; 
      enqueue(res,N) ; 
      enqueue(L,N) ; 
   end loop ; 
   for i in 1..length(right) loop   --puis on place ceux de la file de droite dans la file résultat
      dequeue(R,N) ; 
      enqueue(res,N) ; 
      enqueue(R,N) ; 
   end loop ;
   return res ; 
end ;

Les listes chaînées

Quelques rappels

Comme vous vous en êtes sûrement rendu compte en testant vos fonctions et procédures, l'utilisation des files, si elle semble similaire à celle des piles, est en réalité fort différente. Chacun de ces TAD a ses avantages et inconvénients. Mais le principal défaut de ces TAD est d'être obligé de défiler/dépiler les éléments les uns après les autres pour pouvoir les traiter, ce qui oblige à les rempiler/renfiler par la suite avec tous les risques que cela implique quant à l'ordre des éléments. Notre troisième TAD va donc régler ce souci puisque nous allons traiter des listes chaînées (et ce sera le dernier TAD linéaire que nous traiterons).

Comme dit précédemment, les listes chaînées sont linéaires, doublement chaînées, non cycliques et non contraintes. Qui plus est, elles pourront être traitées en LIFO (comme une pile) ou en FIFO (comme une file) mais il sera également possible d'insérer un élément au beau «milieu» de la liste. Pour cela, il devra être possible de parcourir la liste sans la «démonter» comme nous le faisions avec les piles ou les files.

Heureusement pour vous, le langage Ada intègre, depuis la norme 2005, de nouveaux packages appelés Ada.Containers et qui nous fournissent quelques TAD comme les tables de hachage mais surtout les Doubly_Linked_List (listes doublement chaînées) et les Vectors (vecteurs). Ces deux derniers types sont relativement similaires et correspondent aux listes chaînées. Leur différence ? Les Vectors se comportent un peu à la manière des tableaux, chaque vector étant indexé (en général, indexé avec des entiers naturels commençant à 0 ou 1) de sorte qu'il suffit de disposer du numéro d'indice pour accéder à l'élément voulu, alors que les Doubly_Linked_Lists n'utilisent pas d'indices mais un curseur qui pointe sur un élément de la liste et que l'on peut déplacer vers le début ou la fin de la liste.

Le package Ada.Containers.Doubly_Linked_Lists

Mise en place

Commençons par évoquer le type List. Il est accesible via le package Ada.Containers.Doubly_Linked_Lists. Pour lire les spécifications de ce package, il vous suffit d'ouvrir le fichier appelé a-cdlili.ads situé dans le répertoire d'installation de GNAT. Vous trouverez normalement ce répertoire à l'adresse C:\GNAT sous Windows. Il faudra ensuite ouvrir les dossiers 2011\lib\gcc\i686-pc-mingw32\4.5.3\adainclude (ou quelque chose de ce style, les dénominations pouvant varier d'une version à l'autre).

Comme le package Ada.Numerics.Discrete_Random qui nous servait à générer des nombres aléatoires, le package Ada.Containers.Doubly_Linked_Lists est un package générique (nous verrons bientôt la généricité, patience), fait pour n'importe quel type de donnée et nous ne pouvons donc pas l'utiliser en l'état. Nous devons tout d'abord l'instancier, c'est-à-dire créer un sous-package prévu pour le type de données désiré. Exemple en image :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

with Ada.Containers.Doubly_Linked_Lists ;
...
type T_Score is record
   name  : string(1..3) := "   "; 
   value : natural := 0 ; 
end record ; 

package P_Lists is new Ada.Containers.Doubly_Linked_Lists(T_Score) ; 
use P_Lists ; 

L : List ; 
C : Cursor ;

Primitives

Nous avons ainsi créé un package P_Lists nous permettant d'utiliser des listes chaînées contenant des éléments de type T_Score. Une liste chaînée est de type List (sans S à la fin !). Nous disposons des primitives suivantes pour comparer deux listes, connaître la longueur d'une liste, savoir si elle est vide, la vider, ajouter un élément au début (Prepend) ou l'ajouter à la fin (Append) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

function "=" (Left, Right : List) return Boolean;           --comparaison de deux listes
function Length (Container : List) return Count_Type;       --longueur de la liste
function Is_Empty (Container : List) return Boolean;        --la liste est-elle vide ?
procedure Clear (Container : in out List);                  --vide la liste
procedure Prepend                                           --ajoute un élément en début de liste
  (Container : in out List;
   New_Item  : Element_Type;
   Count     : Count_Type := 1);
procedure Append                                            --ajoute un élément en fin de liste
  (Container : in out List;
   New_Item  : Element_Type;
   Count     : Count_Type := 1);

De même, il est possible de connaître le premier ou le dernier élément (sans le «délister»), de le supprimer, de savoir si la liste contient un certain élément ou pas ou encore d'inverser la liste à l'aide des primitives suivante :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

function First_Element (Container : List) return Element_Type;  --renvoie le premier élément
function Last_Element (Container : List) return Element_Type;   --renvoie le dernier élément

procedure Delete_First                                          --supprime le premier élément
  (Container : in out List;
   Count     : Count_Type := 1);
procedure Delete_Last                                           --supprime le dernier élément
  (Container : in out List;
   Count     : Count_Type := 1);

function Contains                                               --indique si la liste contient cet élément
  (Container : List;
  Item      : Element_Type) return Boolean;

procedure Reverse_Elements (Container : in out List);           --renverse la liste

Ce curseur est là pour nous situer sur la liste, pour pointer un élément. Nous ne pouvons travailler seulement avec le premier et le dernier élément. Supposons que nous ayons la liste suivante :

Le curseur indique le second élément de la liste. Dès lors, nous pouvons lire cet élément, le modifier, insérer un nouvel élément juste avant lui, le supprimer ou bien l'échanger avec un élément pointé par un second curseur avec les primitives suivantes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

function Element (Position : Cursor) return Element_Type; --renvoie l'élément pointé
procedure Replace_Element                                 --modifie l'élément pointé
  (Container : in out List;
   Position  : Cursor;
   New_Item  : Element_Type);
procedure Insert                                          --insère un élément devant l'élément pointé
  (Container : in out List;
   Before    : Cursor;
   New_Item  : Element_Type;
   Count     : Count_Type := 1);
procedure Delete                                          --supprime l'élément pointé
  (Container : in out List;
   Position  : in out Cursor;
   Count     : Count_Type := 1);
procedure Swap                                            --échange deux éléments pointés
  (Container : in out List;
   I, J      : Cursor);

Ce curseur peut être placé au début, à la fin de la liste ou être déplacé élément après élément.

1
2
3
4
5
6
7
8

function First (Container : List) return Cursor;     --place le curseur au début
function Last (Container : List) return Cursor;      --place le curseur à la fin

function Next (Position : Cursor) return Cursor;     --déplace le curseur sur l'élément suivant
procedure Next (Position : in out Cursor);

function Previous (Position : Cursor) return Cursor; --déplace le curseur sur l'élément précédent
procedure Previous (Position : in out Cursor);

Enfin, il est possible d'appliquer une procédure à tous les éléments d'une liste en utilisant un pointeur sur procédure avec :

1

procedure Iterate(Container : List; Process   : not null access procedure (Position : Cursor));

Une application

Nous allons créer un programme créant une liste de 5 scores et les affichant. Je vais vous proposer deux procédures d'affichage distinctes. Mais tout d'abord, créons notre liste :

1
2
3
4
5

Append(L,("mac",500)) ; 
Append(L,("mic",0)) ; 
Append(L,("bob",1800)) ; 
Append(L,("joe",5300)) ; 
Append(L,("mac",800)) ;

Vous avez remarqué, j'ai créé la même liste que tout à l'heure, avec la procédure Append. Une autre façon de procéder, mais avec la procédure Prepend donnerait cela:

1
2
3
4
5

Prepend(L,("mac",800)) ; 
Prepend(L,("joe",5300)) ; 
Prepend(L,("bob",1800)) ; 
Prepend(L,("mic",0)) ;
Prepend(L,("mac",500)) ;

Une dernière méthode (un peu tirée par les cheveux), avec le curseur donnerait :

1
2
3
4
5
6
7

Append(L,("joe",5300)) ; 
C := first(L) ; 
insert(L,C,("mac",500)) ; 
insert(L,("bob",1800)) ; 
previous(C) ;
insert(L,("mic",0)) ; 
Append("mac",500) ;

Enfin, voici une première façon, laborieuse d'afficher les éléments de la liste :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

procedure put(score : T_SCore) is
begin
   Score := Element(C) ; 
   put_line(Score.name & " a obtenu " & integer'image(Score.value) & " points.") ;
end put ; 
…
begin
   C := first(L) ;
   for i in 1..length(L)-1 loop
      put(Element(c)) ; 
      next(c) ; 
   end loop ;
   put(Element(c)) ; 
end ;

Cette première façon utilise le curseur et passe en revue chacun des éléments les uns après les autres. Attention toutefois au cas du dernier élément qui n'a pas de successeur ! À noter également qu'une procédure récursive aurait aussi bien pu faire l'affaire. Enfin, voici une seconde façon de procéder utilisant les pointeurs sur procédure cette fois :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

procedure put(C : Cursor) is
   score : T_SCore; 
begin
   Score := Element(C) ; 
   put_line(Score.name & " a obtenu " & integer'image(Score.value) & " points.") ;
end put ; 
…
begin
   iterate(L,Put'access) ; 
end ;

En utilisant la procédure iterate(), nous nous épargnons ici un temps considérable. Cela justifie amplement les efforts que vous avez fourni pour comprendre ce qu'étaient les pointeurs sur procédure.

Le package Ada.Containers.Vectors

Mise en place

Évoquons maintenant le type vector. Il est accesible via le package Ada.Containers.Vectors. Pour lire les spécifications de ce package, il vous suffit d'ouvrir le fichier appelé a-convec.ads. Encore une fois, ce package doit être instancié de la manière suivante :

1
2
3
4
5
6

with Ada.Containers.Vectors ;
…
package P_Vectors is new Ada.Containers.Vectors(Positive,T_Score) ; 
use P_Vectors ; 

V : Vector ;

Nous créons ainsi un package P_Vectors indexé à l'aide du type Positive (nombre entiers strictement positifs) et contenant des éléments de type T_Score. Nous aurions pu utiliser le type Natural pour l'indexation, mais le type Positive nous garantit que le premier élément du Vector V sera le numéro 1 et non le numéro 0.

Primitives

Les primitives disponibles avec les Doubly_Linked_Lists sont également disponibles pour les Vectors :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

overriding function "=" (Left, Right : Vector) return Boolean; --test d'égalité entre deux vectors
function Length (Container : Vector) return Count_Type;        --renvoie la longueur du vector
function Is_Empty (Container : Vector) return Boolean;         --renvoie true si le vector est vide
procedure Clear (Container : in out Vector);                   --vide le vector
procedure Prepend                                              --ajoute un élément au début du vector
     (Container : in out Vector;
      New_Item  : Vector);
procedure Append                                               --ajoute un élément à la fin du vector
     (Container : in out Vector;
      New_Item  : Vector);
function First_Element (Container : Vector) return Element_Type; --renvoie la valeur du premier élément du vector
function Last_Element (Container : Vector) return Element_Type;  --renvoie la valeur du premier élément du vector
procedure Delete_First                                           --supprimer le premier élément du vector
     (Container : in out Vector;
      Count     : Count_Type := 1);
procedure Delete_Last                                            --supprime le dernier élément du vector
     (Container : in out Vector;
      Count     : Count_Type := 1);
function Contains                                                --indique si un élément est présent dans le vector
     (Container : Vector;
      Item      : Element_Type) return Boolean;
procedure Reverse_Elements (Container : in out Vector);          --renverse l'ordre des éléments du vector

D'autres primitives font appel à un curseur, mais je n'y ferai pas référence (vous pouvez les découvrir par vous même). Mais elles ont en général leur équivalent, sans emploi du curseur mais avec un indice.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

function Element                                   --renvoie la valeur de l'élément situé à l'indice spécifié
     (Container : Vector;
      Index     : Index_Type) return Element_Type;
procedure Replace_Element                          --supprime l'élément situé à l'indice spécifié
     (Container : in out Vector;
      Index     : Index_Type;
      New_Item  : Element_Type);
procedure Insert                                   --insère un nouvel élément avant l'indice spécifié
     (Container : in out Vector;
      Before    : Extended_Index;
      New_Item  : Element_Type;
      Count     : Count_Type := 1);
procedure Delete                                   --supprime l'élément situé à l'indice spécifié
     (Container : in out Vector;
      Index     : Extended_Index;
      Count     : Count_Type := 1);
procedure Swap (Container : in out Vector; I, J : Index_Type); --échange deux éléments
function First_Index (Container : Vector) return Index_Type;   --renvoie l'indice du premier élément
function Last_Index (Container : Vector) return Extended_Index; --renvoie l'indice du dernier élément
procedure Iterate                                  --applique la procédure Process à tous les éléments du Vector
     (Container : Vector;
      Process   : not null access procedure (Position : Cursor));

À ces primitives similaires à celles des listes doublement chaînées, il faut encore en ajouter quelques autres :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

--Fonctions de concaténation
function "&" (Left, Right : Vector) return Vector;
function "&" (Left : Vector; Right : Element_Type) return Vector;
function "&" (Left : Element_Type; Right : Vector) return Vector;
function "&" (Left, Right : Element_Type) return Vector;

procedure Set_Length              --crée un vecteur de longueur donnée
     (Container : in out Vector;
      Length    : Count_Type);
procedure Insert_Space            --insère un élément vide avant l'indice spécifié
     (Container : in out Vector;
      Before    : Extended_Index;
      Count     : Count_Type := 1);
function Find_Index               --trouve l'indice d'un élément dans un tableau
     (Container : Vector;
      Item      : Element_Type;
      Index     : Index_Type := Index_Type'First) return Extended_Index;

Bien sûr, je ne vous ai pas dressé la liste de toutes les fonctions et procédures disponibles, mais vous avez ainsi les principales. À savoir : le type Element_type correspond au type avec lequel vous aurez instancié votre package. De plus, le type Count est une sorte de type integer.

Nous en avons fini avec ce cours semi-théorique, semi-pratique. Nous n'avons bien sûr pas fait le tour de tous les TAD, mais il ne vous est pas interdit (bien au contraire) de développer vos propres types comme des arbres ou des cycles. Cela constitue un excellent exercice d'entraînement à l'algorithmique et à la programmation qui vous poussera à manipuler les pointeurs et à user de programmes récursifs.

En résumé :

• Les TAD ont l'avantage de fournir des conteneurs de taille inconnue et donc non contraints, contrairement aux tableaux. Leur emploi est certes moins évident puisqu'il faut les créer vous-même ou faire appel à un package générique, mais ils résoudront bon nombre de problèmes. Pensez à l'historique de votre navigateur internet, à la liste des items dans un jeu vidéo ou plus simplement aux Unbounded_Strings.
• Si les TAD peuvent très bien être traités par une boucle itérative (LOOP, FOR ou WHILE), leur structure chaînée et leur longueur potentiellement très grande en font des sujets de choix pour les programmes récursifs. Et le besoin de récursivité ne cessera d'augmenter avec la complexité de la structure : imaginez seulement la difficulté de traiter un arbre avec des boucles itératives.
• N'oubliez pas que ces structures ne sont rendues possibles que par l'usage intensif des pointeurs. Si les packages Ada.Container ont été codés avec sérieux, cela ne doit pas vous en faire oublier les risques : évitez, par exemple, d'accéder à un élément d'une liste vide ou de lui retirer un élément !

• Fonctions et procédures II : la récursivité
• Sommaire
• [TP] Le jeu du serpent