Messages postés par "blo yhg"
7 messages sont invisibles car dans un sujet inaccessible.
| Sujet | Date | Extrait |
|---|---|---|
| jeudi 04 janvier 2018 à 22h19 | > J’ai bien un truc sur les espaces vectoriel normés qui dit que tout espace vectoriel normé de dimension finie est compact si et seulement si il est fermé borné. Une *partie* d'un espace vectorie… | |
| jeudi 04 janvier 2018 à 16h01 | > Soit $(z_n)_n\in S$ , on a $\sum_{n\geq 0} z_n^2=1<\infty$ donc le terme générale de cette série $(z_n)^2$ tends vers 0 ce qui implique que la suite $(z_n)_n$ tends vers 0, nous pouvons donc extrai… | |
|
Caf&Sciences
Le coin des scientifiques ! |
samedi 23 décembre 2017 à 22h52 | Hum, bon évidemment beaucoup de monde doit y penser à la blague. Elle est dans la vidéo même : https://youtu.be/VvCytJvd4H0?t=881 |
|
Caf&Sciences
Le coin des scientifiques ! |
samedi 23 décembre 2017 à 22h37 | Tenez j'ai une solution planaire ! :P 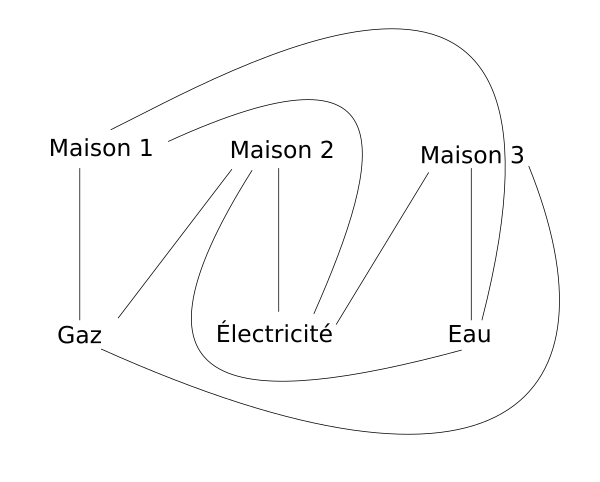 @JuDePom Il y a trois puzzles marrants dans [cette vidéo](https://yout… |
| mardi 12 décembre 2017 à 18h36 | Chez moi ça fonctionne aussi. Si tu cliques [ici](https://zestedesavoir.com/static/smileys/smile.png) et que tu fais ctrl+F5 tu vois la clémentine ? Tu utilises quel navigateur ? | |
| vendredi 08 décembre 2017 à 19h12 | Je propose $\Delta_{\div}$. On trouve [ça](https://math.stackexchange.com/questions/44771/is-there-an-analogue-to-the-delta-symbol-for-ratios) sur math.stackexchange. | |
| vendredi 08 décembre 2017 à 11h13 | [[secret]] | Soit $X$ l'ensemble des parties de $ℕ$ de cardinal $3$. Pour chaque triplet d'ensembles $A_i, A_j, A_k$, on va avoir un point spécial dédié à eux $\{i,j,k\}$ qui va être dans leur inter… | |
| vendredi 08 décembre 2017 à 07h26 | Oui j'ai laissé trop d'implicite à la fin, je vais rectifier. | |
| jeudi 07 décembre 2017 à 20h07 | Un autre qui peut se résoudre en mode "just do it". [[question]] | Montrer qu'il existe une chaîne indénombrable dans l'ensemble des parties de $ℕ$. (C'est-à-dire qu'il existe un ensemble $X$ de … | |
| jeudi 07 décembre 2017 à 18h19 | Bon bah, personne… :( > j’attends que quelqu’un utilise cette technique pour résoudre le problème au dessus (la solution tient en 3-4 lignes ) Tu voulais dire que tu n'attends **pas** une utili… | |
| mardi 05 décembre 2017 à 00h26 | Ouais, et en dimension $n$ ça donne $2^n+1$ points. Le truc célèbre utilisé s'appelle le « principe des tiroirs » : si on a $n+1$ chaussettes distribuées parmi $n$ tiroirs, il y aura obligatoirement … | |
| lundi 04 décembre 2017 à 19h08 | Un indice. [[secret]] | Montrer qu'il y a toujours deux points tels que leur *milieu* soit à coordonnée entières. | |
| samedi 02 décembre 2017 à 21h17 | @entwanne : il faut gérer le cas limite où les valeurs sont réparties entre $n$ et $n+1$ (edit : qui n'est d'ailleurs pas si limite que ça car on arrive dessus dès que le maximum et le minimum n'ont … | |
| vendredi 01 décembre 2017 à 17h13 | *Masqué par blo yhg* | |
| vendredi 01 décembre 2017 à 12h44 | @Asakha Je faisais ça exprès. C'est ta dernière phrase « Petite précision, il n’y a pas de piège etc. » qui m'a donné envie. | |
| vendredi 01 décembre 2017 à 11h12 | @Asakha Malheureusement, aucun prisonnier ne pourra être sauvé car ils ne seront pas suffisamment naïfs pour croire à ce que dit le maton. De toute manière, la première personne refusera de collabore… | |
| vendredi 01 décembre 2017 à 10h49 | > ni même donner une raison Solution temporaire : éditer en remplaçant le message par la raison. | |
| mercredi 29 novembre 2017 à 13h42 | Oui, ça montre que presque tous les réels ne sont pas [calculables](https://en.wikipedia.org/wiki/Computable_number). Chercher "computable analysis", "realizability". *edit* Je voudrais aussi r… | |
| mercredi 29 novembre 2017 à 09h44 | @c_pages Pour avoir quelque chose qui est calculable ou non, il faut commencer par avoir une fonction. Il faut donc une convention sur comment représenter des réels informatiquement et ça peut par ex… | |
| lundi 27 novembre 2017 à 20h29 | Tu poses la question dans un contexte mathématique ou informatique ? Ache t'a fait la réponse informatique. En maths, une fonction $f : A \to B$, c'est un objet mathématique tel que si $a$ est un … | |
| dimanche 26 novembre 2017 à 17h23 | Je ne sais pas quelle est la portée de cette méthode mais ce qu'on peut faire aussi, c'est remplacer les $\overline{x}$ par $1-x$ et développer. Ici, ça donne $bc+bd+cd - 2bcd$. En regroupant, on tro… |