Messages postés par "Freedom"
3 messages sont invisibles car dans un sujet inaccessible.
| Sujet | Date | Extrait |
|---|---|---|
|
Mécanique Quantique : Saut de potentiel et Barrière de potentiel.
Équations différentielles, Effet tunnel |
dimanche 15 octobre 2017 à 11h08 | C'est bien ça. C'est l'interprétation de $|\psi|^2$ comme la densité de probabilité. Tu n'as pas l'impression qu'il y a un *problème* avec cette intégrale si tu utilises la solution $\psi$ que tu … |
|
Mécanique Quantique : Saut de potentiel et Barrière de potentiel.
Équations différentielles, Effet tunnel |
dimanche 15 octobre 2017 à 08h23 | Tu ne réponds pas à la question "quel est la probabilité que la particule soit dans la zone $[-\infty,0]$ ?", tu essaies de deviner la réponse. Quel est le calcul à faire pour y répondre, et que trou… |
|
Mécanique Quantique : Saut de potentiel et Barrière de potentiel.
Équations différentielles, Effet tunnel |
dimanche 15 octobre 2017 à 00h28 | La partie en rouge c'est juste l'exponentielle décroissante que tu trouves avec ta solution : $e^{-\sqrt{2m(V-E)}x/\hbar}$. Ceci dit, je ne sais pas ce que ce graph doit représenter : $\psi$ est … |
| mardi 03 octobre 2017 à 17h59 | Comme point d'entrée, regarde : https://en.wikipedia.org/wiki/Mean_squared_error Je ne garantie pas que l'approche que je propose soit parfaite, mais c'est ce sur quoi je partirais. | |
| mardi 03 octobre 2017 à 17h10 | Comment tu estimes ton $\sigma_A$ ? Pour moi le problème c'est que si ton nombre de réalisations est faible, ton estimation de $\sigma_A$ va être limité. Disons que tu as tes deux lois normales $\… | |
| mardi 03 octobre 2017 à 01h18 | Du coup, disons que tu as deux variables aléatoires (lois normales) $A$ et $B$ (moyennes et variances $\left<A\right>$ et $\sigma_A^2$), tu fais $n$ réalisations de chaque que tu utilises pour estime… | |
| lundi 02 octobre 2017 à 22h26 | Bonjour, Tu as combien de paramètres et de mesures en tout ? Un modèle entre la mesure et les paramètres ? Je ne pense pas que les estimateurs puissent t'aider plus que ça, si ton ensemble n'es… | |
| jeudi 08 juin 2017 à 23h10 | Bonsoir les agrumes, Je suis confronté à un problème numérique que j'ai un peu de mal à aborder. J'ai une fonction $k:\mathbb{R}\mapsto\mathbb{R}$ connue, au besoin on peut rajouter des conditi… | |
| samedi 25 mars 2017 à 15h32 | Bonjour, > On voit très rapidement que cette fonction d'onde n'est pas une fonction propre de l'hamiltonien. Source:[ZDS_M](https://zestedesavoir.com/forums/sujet/8292/variation-dune-fonction-do… | |
|
Une erreur de simplification ? (somme d'Ewald)
Sommes et fonctions trigonométriques |
dimanche 22 mai 2016 à 13h53 | Voila le détail d'où j'étais arrivé : $$\begin{aligned}\sum_{k,i,j}q_i q_j \cos(k.r_{ij}) &= \sum_{k,i,j}\frac{q_i q_j}{2} \left(e^{\imath k.r_{ij}}+e^{-\imath k.r_{ij}}\right) \\ &= \sum_{k,i,j}… |
|
Une erreur de simplification ? (somme d'Ewald)
Sommes et fonctions trigonométriques |
samedi 21 mai 2016 à 23h29 | J'arrive jusque : $\sum_k\left[\left\{\sum_i q_i\sin\left(k.r_i+\frac{\pi}{4}\right)\right\}^2+\left\{\sum_i q_i\sin\left(k.r_i-\frac{\pi}{4}\right)\right\}^2\right]$ En forçant l'introduction … |
|
Une erreur de simplification ? (somme d'Ewald)
Sommes et fonctions trigonométriques |
samedi 21 mai 2016 à 20h18 | Tu dois pouvoir faire ton calcul avec n'importe quel ensemble de $k$ ? Si c'est le cas, avec ```n = [-1, 0., 1., 2.]``` ça ne marche plus. |
| samedi 16 avril 2016 à 16h14 | > De même pour le salarié c'est son salaire net qui compte, pas la répartition des charges. Tu négocie ton salaire net en général, pas le brut. Source:[Demandred](http://zestedesavoir.com/forums/su… | |
| dimanche 13 mars 2016 à 19h44 | Premier message : > dans ce cas plus l'aire à l'intérieur d'une courbe est faible, plus tu es proche d'un extremum. (j'ai oublié de préciser local d'ailleurs) Donc oui pour le volcan c'est pa… | |
| dimanche 13 mars 2016 à 19h34 | Sauf que je n'ai jamais dit qu'un extremum impliquait que l'aire est plus faible, mais qu'une aire plus faible impliquait un extremum. | |
| dimanche 13 mars 2016 à 19h26 | > > Tu vois que les sommets sont là où les lignes de niveau sont le plus serrées. > > Pas vraiment... Les endroits où les lignes de niveaux sont les plus serrées sont les zones les plus pentues (c… | |
| dimanche 13 mars 2016 à 18h41 | Plutôt $\left[0,\infty\right[$. Si tu regardes cette image : 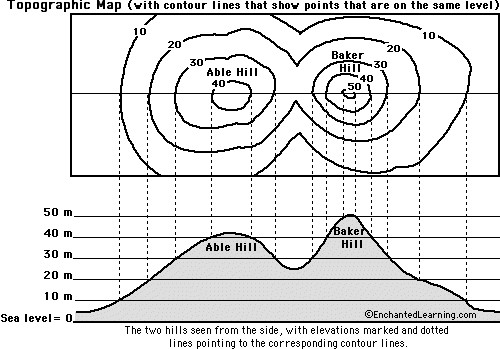 Tu vois que les sommets sont là où les… | |
| dimanche 13 mars 2016 à 15h24 | Bonjour, On est bien d'accord qu'une ligne de niveau est l'ensemble $\left\{\left.\left(x,y\right)\right| f\left(x,y\right)=c\right\}$ ? Dans ce cas je ne vois pas trop pourquoi tu as des lignes d… | |
| vendredi 05 février 2016 à 19h03 | > Or sans prédiction, comme dans le cas présent, on ne peut rien dire de scientifiquement valable. Source:[Holosmos](http://zestedesavoir.com/forums/sujet/5300/ou-se-situe-notre-univers/?page=2#p975… | |
| jeudi 04 février 2016 à 22h36 | > Si deux univers interagissent alors c'est qu'il n'y en a qu'un. Après faudrait faire varier la définition d'univers (déjà on a une distinction entre visible et non visible par exemple). Source:[Ho… | |
| jeudi 04 février 2016 à 19h32 | > > Au risque de poser une bête question : quid s'il existe plusieurs Univers (on aurait donc un modèle de Multivers) comme le suggère certains adeptes de la théorie des cordes (chaque Univers serait… |