Compléments

Comme nous l’avons vu précédemment, les développements limités ont des propriétés très agréables. Par exemple, les développements limités du produit, de la somme et de la composition sont respectivement les produit, somme et composition des développements limités.

Mais il y a certaines propriétés qui ne sont pas vérifiées. Par exemple, admettre un développement limité à l’ordre $n$ ne permet pas de dire que $f$ est de classe $C^n$ pour $n\geq 2$ alors que c’est bien le cas pour $n=0$ ou $n=1$.

Contre-exemples

Sur la relation « être négligeable devant »

$o(\cdot)$ n’est pas compatible avec l’addition. En effet, on a au voisinage de $x= +\infty$ : $x = x^3\frac{1}{x^2} = o(x^3)$

et $-x^2 = -x^3\frac{1}{x}= o(-x^3)$

mais on a pas $x-x^2 = o(0)$ puisque $x-x^2$ ne tend pas vers $0$ en l’infini.

Un développement limité à l’ordre $n$ n’implique pas $C^n$

On considère l’application $f$ au voisinage de $x=0$ définie par $f(0) = 0$ et $\forall x \neq 0, \; f(x) = x^3\sin(1/x).$

$f$ est bien continue en $0$. En définissant $\epsilon$ par $\epsilon(0) = 0$ et $\forall x \neq 0, \epsilon(x) = x \sin(1/x),$

$\epsilon$ est continue en $0$ et on a $f(x) = x^2 \epsilon(x)$

ce qui montre que $f$ admet comme développement limité à l’ordre $2$ en $x= 0$ : $f(x) = o(x^2).$

Maintenant il suffit de montrer que $f$ n’est pas dérivable en $0$ deux fois alors qu’elle y admet un développement limité à l’ordre $2$.

On a $\forall x \neq 0, \; \frac{f(x) - f(0)}{x-0} = x^2\sin(1/x)$

et donc $f$ est dérivable en $0$ et $f'(0) = 0$. De plus pour tout $x\neq 0$ on a que $f$ est dérivable en $x$ et $f'(x) = 3x^2\sin(1/x) - x\cos(1/x).$

Mais : $\forall x\neq 0, \; \frac{f'(x) - f'(0)}{x-0} = \frac{3x^2\sin(1/x) - x\cos(1/x)}{x} = 3x\sin(1/x) - \cos(1/x)$

ce qui montre que $f'$ n’est pas dérivable en $0$ puisque $\cos(1/x)$ n’admet pas de limite en $0$.

Les développements limités qui suivent sont tous au voisinage de $x=0$. Ils sont à connaître ou à savoir retrouver rapidement.

Soit $n\in \mathbf{N}$ et soit $a\in\mathbf{R}$.

• $\displaystyle (1+x)^a = 1 + a\cdot x + \frac{a(a-1)}{2}x^2 + \ldots + \frac{a(a-1)\cdots (a-n+1)}{n!}x^n + o(x^n)$
• $\displaystyle\frac{1}{1-x} = \sum_{k=0}^n x^k + o(x^n)$
• $\displaystyle\ln(1-x) = -\left(\sum_{k=1}^n \frac{x^k}{k}\right) + o(x^n)$
• $\displaystyle\exp(x) = \sum_{k=0}^n \frac{x^k}{k!} + o(x^n)$
• $\displaystyle\cos(x) = \sum_{k=0}^n (-1)^k\frac{x^{2k}}{(2k)!}+ o(x^{2n+1})$
• $\displaystyle\sin(x) = \sum_{k=0}^n (-1)^k\frac{x^{2k+1}}{(2k+1)!}+ o(x^{2n+2})$

En principe, les autres développements limités usuels (fonctions hyperboliques par exemple) sont faciles à retrouver à partir de ces développements et des règles d’opérations sur les développements limités (pour former tangente par exemple).

Dans cette dernière partie, on va essayer d’appliquer tout ce que l’on a appris à des cas plus « concrets ».

Nous allons en aborder deux, une étude de limite et l’approximation d’un nombre.

Étude de limite

On va essayer d’établir l’existence et la valeur de la limite : $\lim_{x\to 0} \frac{1}{x^2} - \frac{1}{(\sin(x))^2}.$

On remarque tout d’abord qu’il s’agit bien d’une forme indéterminée puisque $\lim \frac{1}{x^2} = +\infty$ et $\lim \frac{-1}{(\sin(x))^2} = -\infty$. On considère à partir de maintenant les limites en $0$, ce qui permet d’alléger l’écriture.

Il va s’agir de faire un développement limité du second terme. Pour rappel $\sin(x) = x - \frac{x^3}{6} + \frac{x^5}{5!} + \ldots + \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+2}).$

Si on ne développe qu’à l’ordre $n=1$ on va se retrouver à la situation suivante : $\lim \frac{1}{x^2} - \frac{1}{x^2 + o(x^2)} =\lim \frac{x^2 + o(x^2) - x^2}{x^2(x^2+o(x^2))}= \lim \frac{o(x^2)}{x^4+o(x^4)}$

ce qui est encore une forme indéterminée puisque le numérateur et le dénominateur tendent vers $0$.

On va donc développer à l’ordre $n=4$ en $x=0$ : $\sin(x) = x - \frac{x^3}{6} + o(x^4), \; (\sin(x))^2 = x^2 - \frac{x^4}{3} + o(x^4).$

Ainsi : $\lim\frac{1}{x^2} - \frac{1}{(\sin(x))^2} = \lim \frac{1}{x^2} - \frac{1}{x^2(1 - \frac{x^2}{3} + o(x^2))} = \lim \frac{1}{x^2}\left( 1 - \frac{1}{1-x^2/3 + o(x^2)}\right).$

Mais quand $x$ tend vers $0$ on a que $1-x^2/3 + o(x^2)$ tend vers $1$ et donc on peut faire un développement limité de $\frac{1}{1-x^2/3 + o(x^2)}$ en $x=0$. Pour rappel quand $X$ est au voisinage de $0$ : $\frac{1}{1-X} = 1 + X +o(X)$

et donc au voisinage de $x=0$ $\frac{1}{1-x^2/3 + o(x^2)} = 1 +x^2/3 + o(x^2).$

Ainsi, $\lim \frac{1}{x^2} - \frac{1}{(\sin(x))^2} = \lim \frac{1 -( 1 +x^2/3 + o(x^2))}{x^2} = \lim \frac{-x^2}{3x^2} + o(1) = \lim \frac{-1}{3} + o(1) = \frac{-1}{3}.$

Conclusion : on a établi que $\lim_{x\to 0} \frac{1}{x^2} - \frac{1}{(\sin(x))^2} = -\frac{1}{3}$

ce qui est loin d’être évident a priori !

Approximation

On va donner une méthode d’approximation du nombre $e=\exp(1)$, la base du logarithme népérien. Pour cela on va utiliser l’encadrement du reste de la formule de Young-Lagrange.

On commence par développer $\exp(x)$ au voisinage de $x=0$ à l’ordre $n$. On a : $\exp(x) = \sum_{k=0}^n\frac{x^k}{k!} + R_{n+1}(x)$

et on a qu’il existe $\theta$ entre $0$ et $1$ tel que $R_{n+1}(x) = \frac{x^{n+1}}{(n+1)!} \exp(\theta x)$

mais comme $\theta \leq 1$ on a $\exp(\theta x)\leq \exp(x)$ et donc finalement $|\exp(1) - R_{n+1}(1) | \leq \frac{e}{(n+1)!}$

ce qui très, très petit !

Pour vous donner une idée plus précise de l’ordre de grandeur de $1/n!$ on a : $\frac{1}{5!} \simeq 0.008, \; \frac{1}{8!} \simeq 0.00002.$

Une approximation grossière de $e$ donne $e\leq 3$. Ainsi, en développant à l’ordre $7$ on aurait un reste de moins de un millième !

Or, on peut calculer aisément : $\sum_{k=0}^7 \frac{1}{k!} = 1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} + \frac{1}{720} + \frac{1}{5040} = \frac{685}{252}$

cela donne : $e \simeq 2.7182$

et on sait que la troisième décimale est exacte.

Maintenant que vous savez faire des développements limités et que vous savez à quoi cela peut servir, on peut se poser une question simple.

Est-ce qu’un développement limité qui donne un polynôme nul à tout ordre, implique que la fonction développée est localement nulle ?

Nous allons voir qu’en analyse réelle c’est faux : il existe des fonctions dites « plates » dont le développement limité à tout ordre en un certain $a\in\mathbf{R}$ donne un polynôme nul sans que la fonction soit nulle localement.

Définition formelle

Soit $f : V\to\mathbf{R}$ une fonction numérique, supposée $C^\infty$ et où $V$ un voisinage de $a\in\mathbf{R}$.

---

Définition

$f$ est dite plate si pour tout $n\in\mathbf{N}$ et tout $h$ suffisamment petit pour que $a+h\in V$ on a : $f(a+h) = o(h^n).$

---

Par exemple, le plus trivial qui existe, $f=0$, la fonction identiquement nulle sur $\mathbf{R}$ est plate.

Nous allons donner deux exemples non triviaux de telles fonctions. Le premier exemple doit vous rester à l’esprit, il est important dans d’autres problématiques en analyse.

Exemples

Premier exemple

On considère $V = \mathbf{R}$ et la fonction $f$ définie par $f(0) = 0$ et
$f(x)= \exp\left(-\frac{1}{x^2}\right)$

pour tout $x$ non nul.

Vous pouvez vérifier que $f$ est bien $C^\infty$ et que pour tout $n\in\mathbf{N}$, $f^{(n)}(0) = 0$. Ainsi, on a bien pour tout $n\in\mathbf{N}$ : $f(h) = o(h^n)$

pour tout $h$ réel.

Cependant, remarquez que $f$ ne s’annule qu’en $0$. En effet, pour tout $x$ non nul, $\exp(-1/x^2)$ ne s’annule pas.

Voici, graphiquement, à quoi cette fonction ressemble :

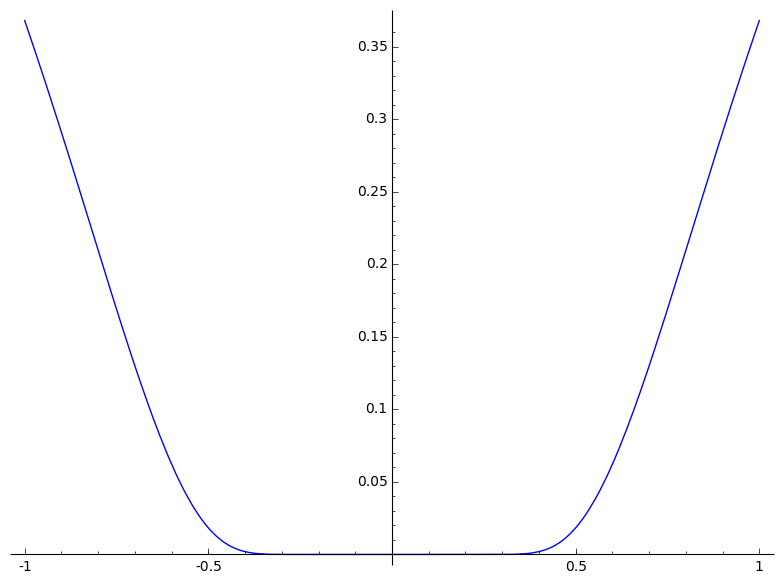
La dénomination « plate » devrait s’éclaircir : on a vraiment l’impression que la courbe s’aplatit sur $y=0$.

Deuxième exemple

Une autre manière de faire une fonction plate est d’utiliser un objet qui n’a pas été présenté : la série de Taylor d’une fonction $C^\infty$. Il m’est impossible de traiter de cet objet ici, cependant vous pouvez le penser comme une généralisation des développements limités à l’ordre $n = +\infty$.

Nous allons nous baser sur la fonction suivante : $f: x\mapsto \frac{1}{1-x}$

qui est définie dans un voisinage de $0$. En particulier, elle est bien définie sur $]-1,1[$.

Un simple calcul montre que pour tout $n\in\mathbf{N}$ et tout $h\in ]-1,1[$, : $f(h) = \sum_{k=0}^n h^k + o(h^n).$

On va considérer la « série entière » : $S(x) = \sum_{k\geq 0}x^k.$

On dit que $S$ est simplement convergente en $x$ lorsque la suite de ses sommes partielles : $\left(\sum_{k=0}^n x^k \right)_{n\in\mathbf{N}}$

converge.

Or on peut montrer très facilement que $S$ converge simplement sur $]-1,1[$. En effet, vous connaissez sans doute la formule : $\sum_{k=0}^n x^k = \frac{1-x^{n+1}}{1-x}$

valable pour tout $x\in ]-1,1[.$ En particulier, on peut faire tendre $n$ vers $+\infty$, ce qui fait tendre $x^{n+1}$ vers $0$ et montre que : $S(x) = \sum_{k=0}^{+\infty}x^k = \frac{1}{1-x}$

pour tout $x\in]-1,1[$.

Maintenant on peut se demander ce qui se passe en dehors de $]-1,1[$.

Par des outils d’analyse des séries numériques, vous pourriez montrer assez facilement que $S(x)$ diverge très vite pour $x$ tel que $|x|\geq 1$. En effet, remarquez que $|x|^k$ ne tend pas vers $0$ quand $k$ tend vers $+\infty$. Cela empêche la suite des sommes partielles de converger !

Et pourtant, $f$ est bien définie pour $x\neq 1$. On arrive donc à une bifurcation : la série $S$ n’a plus de valeur finie pour $|x|\geq 1$ et pourtant $f$ est bien définie pour $|x|\geq 1$ et $x\neq 1$.

On peut regarder graphiquement ce qu’il se passe. Bien évidemment, je ne peux pas calculer $S(x)$ pour $|x|>1$. Je vais donc tricher un peu et considérer l’application : $g(x) = \sum_{k=0}^{\eta-1} x^k = \frac{1-x^\eta}{1-x}$

et je prends $\eta = 10^6$.

Je trace en bleu l’application $f$ sur $[-1,1]$ (une asymptote verticale bleue apparaîtra en $x=1$) et en rouge $f-g$ sur $[-1,1]$.

J’observe la chose suivante :

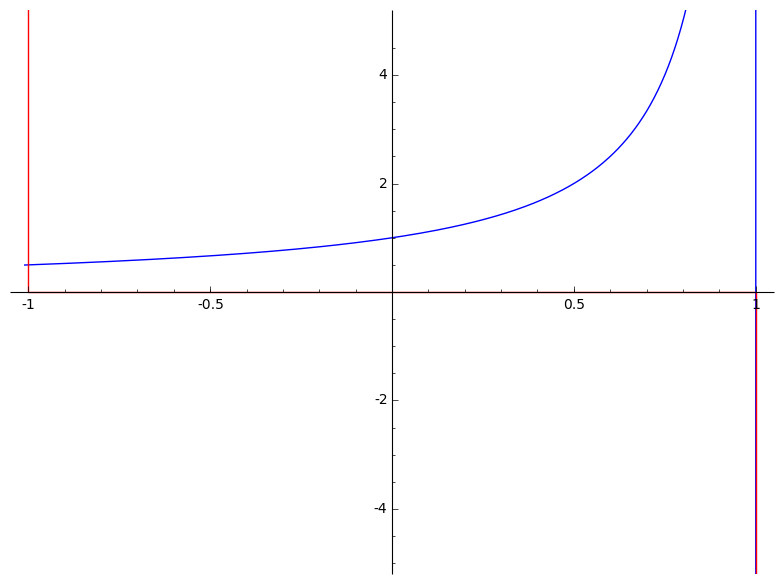
On se rend bien compte que $f-g$ est plate dans un voisinage de $0$ mais « explose » (elle part à l’infini) dès que $|x|\geq 1$.