Nous avons introduit le principe de la somme de contrôle dans le chapitre « Aujourd’hui, contrôle ! ». Si vous êtes curieux, nous allons explorer un peu le côté technique de ce mécanisme dont la vocation est, comme l’indique le titre, la détection d’erreurs. Enjoy !
- La vérification de parité
- La somme de contrôle de Fletcher
- L’algorithme Adler-32
- Quand IP rime avec simplicité
La vérification de parité
Bienvenue à votre premier baptême du feu.
Comme l’indique le titre, nous allons débuter notre exploration des algorithmes de computation de somme de contrôle en étudiant l’algorithme de vérification longitudinale de parité.
La parité, c’est quand il y a autant d’hommes que de femmes ?
La parité est la propriété de tout nombre dont le reste d’une division par 2 est un nombre entier. En d’autres termes, on appelle nombre pair tout nombre qui est multiple de deux. Tout le monde ici sait qu’est-ce qu’un nombre pair et impair, quand même ?
Un algorithme de vérification longitudinale de parité se base sur la parité. Mais pas la parité des nombres entiers : il se base sur la parité de bits.
Des bits ? Des 0 et 1 pairs ?
D’abord on se calme, n’ayez pas peur.
La parité de bit ou le bit de parité, c’est la forme la plus simple de détection d’erreur. Ne commencez pas tout de suite à paniquer, l’algorithme de vérification de parité est plus simple à comprendre que les autres à venir.
Imaginez que vous avez une suite de bits 10011001. Cette suite de bits a 4 bits allumés (4 bits qui valent 1). Pour nous les humains, nous savons par expérience que 4 est un nombre pair, nous n’avons pas besoin de faire des calculs pour vérifier la parité de ce nombre. Mais pour un ordinateur qui fonctionne avec des 0 et 1, comment savoir que 4 est pair ? Comment savoir que l’ensemble des bits allumés dans une suite de bits est un nombre pair ? On utilise pour ce faire un bit de parité.
En toute logique, il y a deux types de bit de parité : le bit de parité pair et le bit de parité impair.
Ça ne nous dit pas ce qu’est un bit de parité…
Un bit de parité est un bit ( si si ) que l’on ajoute au début d’une suite de bits pour nous informer de la parité du nombre de bits allumés. C’est un peu difficile à comprendre, nous vous l’accordons, mais nous sommes là pour vous simplifier cela au maximum.
Prenons une suite de bits 1001111. Cette suite de bits a 5 bits allumés, c’est-à-dire 5 bits qui valent 1. Nous allons ajouter un bit au début de cette suite. Ce bit va déterminer si 5 est pair ou impair. Ce bit ajouté, c’est cela le bit de parité.
C’est quoi la différence entre le bit parité pair et le bit de parité impair ?
Bonne question ! Chacun de ces deux bits sert à déterminer la parité d’un nombre, c’est-à-dire déterminer si le nombre de bits allumés est un nombre pair ou impair. Mais quelle est la différence entre ces deux bits ?
Le bit de parité pair
Bien. Quand vous utilisez un bit de parité pair, le bit de parité qui sera ajouté à votre suite de bits aura pour valeur 1 si le nombre de bits allumés est impair.
Un exemple ? Prenons la suite 1111111. Nous avons 7 bits et 7 est un nombre impair. Le bit de parité sera donc 1.
Retenez ceci : l’ajout du bit de parité pair rendra l’ensemble des bits allumés pair. 7 est un nombre impair, n’est-ce pas ? Notre bit de parité pair doit donc valoir 1. Et si nous ajoutons 7 bits allumés + le bit de parité pair, ça donne 8 bits et 8 est un nombre pair. Donc ajouter un bit de parité pair rendra toujours l’ensemble des bits allumés pair.
Le bit de parité impair
Si vous utilisez un bit de parité impair, le bit doit valoir 1 si l’ensemble des bits allumés est pair.
Un exemple ? 1101100. Cette suite a 4 bits allumés et 4 est un nombre pair, donc le bit de parité impair que l’on ajoutera à cette suite vaudra 1. Contrairement au bit de parité pair, celui-ci rendra l’ensemble des bits impair. 4 est pair, si on ajoute un bit de parité impair (qui vaut 1) on se retrouve donc avec 5 bits allumés, et 5 est un nombre impair.
En résumé, retenez la règle suivante :
Soit S, une suite de bits composée de n bits allumés. Un bit de parité pair aura pour valeur 0 si n est un nombre pair. Un bit de parité impair aura pour valeur 0, si n est un nombre impair.
Il est vraiment important de comprendre le principe du bit de parité (pair ou impair), car c’est le principe de base de l’algorithme de vérification longitudinale de parité. C’est d’ailleurs important pour comprendre le contrôle de redondance cyclique.
Nous allons donc faire quelques exercices : 3 exercices pour le bit de parité pair et 3 autres pour le bit de parité impair. C’est parti ! :pirate :
Exercices sur le bit de parité pair
Commençons par quelque chose de très simple : 1110000. Voilà une suite de bits qui a 3 bits allumés. Nous voulons utiliser un bit de parité pair. Nous savons que le bit de parité pair vaut 1 si et seulement si le nombre de bits allumés est un nombre impair. Ça tombe bien parce que 3 est impair. Donc nous allons réécrire cette suite de bits en intégrant le bit de parité pair. Le bit de parité pair rendra le nombre de bits allumés pair comme nous l’avons vu. Le bit de parité se place au début de la suite de bits.
11110000
Voilà, c’est fait. Nous avons désormais 4 bits allumés, ce qui est un nombre pair, car l’ajout du bit de parité pair rendra toujours l’ensemble des bits allumés pair.
Deuxième exercice !
Soit la suite de bits 1111100. Nous avons 5 bits allumés. Notre bit de parité pair devra donc valoir 1 puisque 5 est impair.
11111100
Nous avons désormais 6 bits allumés et 6 est un nombre pair.
Un dernier exercice pour la route !
Soit la suite 1100000. 2 est un nombre pair. Or le bit de parité pair prend la valeur 1 si et seulement si le nombre de bits allumés est impair. Il s’avère que 2 n’est pas impair, donc le bit de parité ne peut pas être allumé. Il aura pour valeur 0.
Nous avons fait exprès de vous faire voir ce cas. Si le nombre de bits allumés est un nombre pair, il vaudra 0, sinon il vaudra 1 comme nous l’avons fait pour les premiers exercices. Allez, écrivons cette suite avec le bit de parité.
01100000
Remarquez que n (le nombre de bit allumés, 2 en l’occurrence) + 0 (le bit de parité pair) nous donne toujours un nombre pair pour respecter la règle.
Exercices sur le bit de parité impair
Vous vous souvenez de la règle ? Le bit de parité impair vaut 1 lorsque le nombre de bits allumés est un nombre pair, sinon il vaut 0. Cela veut dire que si le nombre de bits allumés est un nombre impair, le bit de parité impair vaudra 0.
Sans plus tarder, commençons.
Soit la suite 1100000. Cette suite a 2 bits allumés. 2 est un nombre pair, donc le bit de parité impair vaudra 1. Écrivons cela :
11100000
Remarquez que nous avons désormais 3 bits allumés et 3 est un nombre impair. Ça confirme bien la règle : l’ajout d’un bit de parité impair rendra impair le nombre de bits allumés.
Continuons !
Soit la suite 1010100. Nous avons 3 bits allumés. 3 est impair, par conséquent le bit de parité vaudra 0. Cela nous donne :
01010100.
Pour terminer, considérons la suite 1111110. 6 est un nombre pair, donc le bit de parité impair vaudra 1. Nous sommes des pros maintenant, ça devrait couler de source :
11111110
Conclusion
Le principe des bits de parité sert de base à d’autres opérations plus complexes. Ce système est aussi utilisé tel quel dans certains protocoles de niveau 2, nous aurons certainement l’occasion d’en reparler.
Pour conclure, il y a 4 règles d’or à retenir :
- Un bit de parité pair vaut 1 lorsque le nombre de bits allumés dans une suite est un nombre impair. Sinon il vaut 0.
- L’ajout d’un bit de parité pair à une suite donnera un nombre pair de bits allumés.
- Un bit de parité impair vaut 1 lorsque le nombre de bits allumés dans une suite est un nombre pair. Sinon il vaut 0.
- L’ajout d’un bit de parité impair à une suite donnera un nombre impair de bits allumés.
La somme de contrôle de Fletcher
Le bit de parité, c’est assez simple, c’est rapide à calculer, mais ce n’est pas très performant. Ce serait mieux d’avoir une information plus fiable. D’un autre côté, on ne veut pas non plus avoir des méthodes qui sont couteuses en ressources et en temps.
Jusqu’au début des années 1980, un système de somme de contrôle assez simple était utilisé. Il consiste à découper le message à transmettre en blocs de taille fixe (1 octet, 2 octets, 4 octets, …). On fait ensuite la somme des valeurs de chacun de ces blocs.
Prenons pour exemple le mot « Bonjour », encodé en ASCII1. Découpons-le en blocs de 1 octet. On obtient les valeurs suivantes :
| B | o | n | j | o | u | r |
|---|---|---|---|---|---|---|
| 066 | 111 | 110 | 106 | 111 | 117 | 114 |
La somme de toutes ces valeurs donne… Quelqu’un aurait une calculatrice ? 735. On ajoute cette valeur au bout du message.
Mais comment le destinataire sait quelle partie du message correspond à la somme de contrôle ?
Ça, c’est défini en amont par le protocole utilisé ! Dans notre exemple, on va supposer que seul le dernier octet correspond à la somme de contrôle.
Ça ne peut pas aller ! On ne peut pas stocker la valeur 735 sur un seul octet, il en faut 2 !
C’est exact. On commence à mettre le doigt sur une importante problématique. Même si c’était deux octets, pour peu que le message soit long, on pourrait dépasser la valeur maximale de 65535. Alors comment faire ?
C’est là qu’intervient l’arithmétique modulaire. Ce concept mathématique introduit la fonction modulo. Le modulo, c’est une opération qui consiste à conserver le reste d’une division entre deux nombres entiers. On note cette opération mod ou, dans certains langages de programmation, %. Ainsi, 10 mod 3 = 1, car le reste de la division de 10 par 3 est 1. Essayez de résoudre ces opérations de tête pour vous entrainer :
- 13 mod 4 = ?
- 50 mod 10 = ?
- 735 mod 256 = ?
Afficher/Masquer le contenu masqué
- 13 mod 4 = 1, car 13 / 4 = 3 et il reste 1
- 50 mod 10 = 0, car 50 / 10 = 5 et il reste 0
- 735 mod 256 = 223, car 735 / 256 = 2 et il reste 223
Quel rapport avec la somme de contrôle ?
Regardez la dernière opération que vous avez calculée. Vous avez réussi à faire rentrer la valeur 735 sur un octet ! Bon, pas tout à fait. À partir de la somme calculée, nous avons obtenu une valeur que nous n’aurions pas obtenue avec un autre message. S’il y avait eu une erreur de transmission, par exemple sur le dernier bit de la 4ème lettre du message, le « j » serait devenu un « k », et la valeur numérique décimale serait 107 et non 106. La somme des valeurs serait 736 et non 735. L’opération modulo aurait été 736 mod 256 = 224, et non 223. Le récepteur aurait donc calculé une somme de contrôle différente de celle fournie par l’expéditeur, c’est-à-dire 223, qui a été jointe au message d’origine. On sait donc qu’il y a forcément eu une erreur de transmission.
Cette méthode est pratique, car elle est assez simple et rapide à calculer. Toutefois, elle n’est pas très fiable : on peut tomber sur le bon résultat malgré des erreurs de transmission. C’est ce qu’on appelle une collision. Pire encore : on tombera quand même sur la bonne somme de contrôle avec les blocs (dans notre exemple, les lettres) inversées.
Nous avons choisi le diviseur 256 dans notre exemple. Cela permet de s’assurer que la somme de contrôle rentrera sur un octet. En effet, tout nombre modulo 256 ne peut pas donner un résultat supérieur à 255, qui est la valeur maximale stockable sur un octet. On peut aussi choisir un diviseur inférieur, cela fonctionnerait de la même manière. Par contre, les chances de collision seront supérieures, puisque le nombre total de valeurs possibles sera réduit. Si nous avions choisi de stocker notre somme de contrôle sur 2 octets, nous aurions pu choisir un diviseur allant jusqu’à 65536.
Un Fletcher sauvage apparait !
Vers la fin des années 1970, le physicien John Fletcher, du laboratoire national de Lawrence Livermore en Californie, propose une amélioration à ce système. Il consiste à ajouter, en plus de la somme de contrôle étudiée précédemment, la somme de toutes les étapes intermédiaires. Ainsi, cela permet de prévenir l’inversion de blocs lors de la transmission et réduit le risque de collision. Comme c’est difficile à visualiser, faisons tout de suite un exemple.
Reprenons le message sur lequel nous avons travaillé. Nous allons calculer, étape par étape, deux sommes de contrôle : celle d’origine, et celle de Fletcher, qui consiste à additionner la première checksum à chaque étape. Nous conservons la même taille de bloc et le même modulo, que nous appliquerons à chaque étape pour plus de lisibilité (cela ne change rien que cette opération soit faite à la fin ou au fur et à mesure).
| B | o | n | j | o | u | r |
|---|---|---|---|---|---|---|
| 066 | 111 | 110 | 106 | 111 | 117 | 114 |
Étape | Bloc | Checksum 1 | Checksum 2 |
|---|---|---|---|
1 | B | 66 | 66 |
2 | o | 66 + 111 = 177 | 66 + 177 = 243 |
3 | n | 177 + 110 = 287 287 mod 256 = 31 | 243 + 31 = 274 274 mod 256 = 18 |
4 | j | 31 + 106 = 137 | 18 + 137 = 155 |
5 | o | 137 + 111 = 248 | 155 + 248 = 403 403 mod 256 = 147 |
6 | u | 248 + 117 = 365 365 mod 256 = 109 | 147 + 109 = 256 256 mod 256 = 0 |
7 | r | 109 + 114 = 223 | 0 + 223 = 223 |
On retrouve bien la somme de contrôle initiale, 223, comme calculé auparavant. La somme de contrôle de Fletcher nous donne aussi 223, ce qui est un hasard. Un protocole qui utilise cet algorithme ajoutera ces valeurs à la fin du message.
| Octet 1 | Octet 2 | Octet 3 | Octet 4 | Octet 5 | Octet 6 | Octet 7 | Octet 8 | Octet 9 |
|---|---|---|---|---|---|---|---|---|
| B | o | n | j | o | u | r | 223 | 223 |
Nous avons évoqué le fait que l’ajout de cette seconde somme de contrôle réduit les risques de collision. En effet, avec une somme de contrôle basique, deux erreurs peuvent se neutraliser et donner quand même le bon résultat, notamment si deux blocs sont inversés. Avec Fletcher, comme la deuxième checksum conserve en quelque sorte un historique des opérations, cela devient fort peu probable. Voyons ce qu’il se passe si, dans notre exemple, deux lettres se retrouvent inversées lors de la transmission.
| Octet 1 | Octet 2 | Octet 3 | Octet 4 | Octet 5 | Octet 6 | Octet 7 | Octet 8 | Octet 9 |
|---|---|---|---|---|---|---|---|---|
| B | o | j | n | o | u | r | 223 | 223 |
| B | o | j | n | o | u | r |
|---|---|---|---|---|---|---|
| 066 | 111 | 106 | 110 | 111 | 117 | 114 |
Étape | Bloc | Checksum 1 | Checksum 2 |
|---|---|---|---|
1 | B | 66 | 66 |
2 | o | 66 + 111 = 177 | 66 + 177 = 243 |
3 | j | 177 + 106 = 283 283 mod 256 = 27 | 243 + 27 = 270 270 mod 256 = 14 |
4 | n | 27 + 110 = 137 | 14 + 137 = 151 |
5 | o | 137 + 111 = 248 | 151 + 248 = 399 399 mod 256 = 143 |
6 | u | 248 + 117 = 365 365 mod 256 = 109 | 143 + 109 = 252 |
7 | r | 109 + 114 = 223 | 252 + 223 = 475 475 mod 256 = 219 |
Cette erreur de transmission n’a pas été détectée par la somme de contrôle simple, mais est repérée par celle de Fletcher : on trouve comme résultat 219 au lieu de 223. On sait donc que le message n’est pas bon et qu’il ne faut pas le prendre en compte.
La facilité de calcul de cet algorithme et sa relative fiabilité lui ont valu d’être publié en 1982 dans la revue IEEE Transactions on Communications, qui est la référence dans le domaine des télécommunications. En 1990, une proposition a été émise pour qu’il puisse être utilisé dans TCP, mais cela n’a pas abouti. En 2018, les systèmes de fichiers ZFS et APFS utilisent toujours l’algorithme de Fletcher. Ce dernier a inspiré d’autres personnes, comme Mark Adler, qui en a proposé sa propre version.
- L'ASCII est une norme qui fait correspondre des caractères, comme des lettres, à des nombres, exploitables par les ordinateurs. En ASCII, la lettre A correspond au nombre 65, le B à 66, etc.↩
L’algorithme Adler-32
L’algorithme de Fletcher permet, en théorie, une certaine souplesse : on peut découper les messages en des blocs de la taille qu’on veut (1 octet, 2 octets, …), on peut choisir sur combien d’octets tiendra la somme de contrôle, etc. En 1995, l’ingénieur américain Mark Adler propose cette configuration particulière :
- Chaque somme de contrôle est calculée sur 2 octets ;
- La checksum 1 prend pour valeur de départ 1, tandis que la checksum 2 part de 0 ;
- Une opération est réalisée pour chaque bloc de 8 bits, soit 1 octet ;
- Le diviseur utilisé pour les modulos est 65521 ;
- Au bout du message à transmettre, la checksum 2 est inscrite avant la checksum 1.
Reprenons notre exemple et appliquons l’algorithme Adler-32.
| B | o | n | j | o | u | r |
|---|---|---|---|---|---|---|
| 066 | 111 | 110 | 106 | 111 | 117 | 114 |
Étape | Bloc | Checksum 1 | Checksum 2 |
|---|---|---|---|
1 | B | 1 + 66 = 67 | 67 |
2 | o | 67 + 111 = 178 | 67 + 178 = 245 |
3 | n | 178 + 110 = 288 | 245 + 288 = 533 |
4 | j | 288 + 106 = 394 | 533 + 394 = 927 |
5 | o | 394 + 111 = 505 | 927 + 505 = 1.432 |
6 | u | 505 + 117 = 622 | 1.432 + 622 = 2.054 |
7 | r | 622 + 114 = 736 | 736 + 2.054 = 2.790 |
Le message transmis est alors :
Octet 1 | Octet 2 | Octet 3 | Octet 4 | Octet 5 | Octet 6 | Octet 7 | Octet 8 | Octet 9 | Octet 10 | Octet 11 |
|---|---|---|---|---|---|---|---|---|---|---|
B | o | n | j | o | u | r | 2.790 | 736 | ||
Ce paramétrage utilise la valeur 65521 pour les modulos. Dans notre exemple, nous n’atteignons pas cette valeur, donc nous le visualisons pas. Sans rentrer dans les détails, l’utilisation de ce nombre premier réduit le risque de collision. Toutefois, cette configuration rend l’exécution de l’algorithme plus lente que la plupart des paramétrages communs de Fletcher.
Pourquoi on en parle, alors ?
Eh bien voyez-vous, Adler-32 est très utilisé. Mais vraiment très, très utilisé. Et pour cause : on le retrouve dans zlib, une bibliothèque logicielle qui est utilisée pour la compression de pas mal de choses, comme les archives ZIP ou les images PNG. Ce programme est un composant essentiel de bon nombre de systèmes d’exploitation et de consoles de jeu du 21ème siècle.
Et vous vous demandez, pourquoi Adler-32 se retrouve dans zlib ? C’est très simple : zlib a été créée par 2 ingénieurs, le polytechnicien français Jean-loup Gailly… et un certain Mark Adler. Tant qu’à faire, les deux compères ont aussi créé gzip, un format de compression utilisé sur la couche 6 (présentation) du modèle OSI.
Ces deux algorithmes, Fletcher et Adler, ont pour avantages la simplicité et la rapidité d’exécution, mais ne sont pas totalement fiables. De plus, ils permettent de détecter une erreur dans un message, mais pas de la localiser et encore moins de la corriger. Pour cela, on préférera utiliser un contrôle de redondance cyclique.
Quand IP rime avec simplicité
Cette section est liée au chapitre sur le protocole IP. Il est recommandé de connaitre l’en-tête IPv4 avant de poursuivre.
Le protocole IP dans sa version 4 utilise une somme de contrôle, mais pour l’en-tête des paquets uniquement. Le principe est relativement simple : on découpe le header par blocs de 16 bits, et on les additionne tous. Pour faciliter les choses, on écrira ces calculs en binaire. Si le résultat s’écrit sur plus de 16 bits, on découpe et on additionne encore, mais en commençant par la droite. On termine en inversant la valeur de chaque bit et on a la somme de contrôle de l’en-tête IP.
Faisons un exemple en prenant un paquet IP reproduit dans le tableau ci-dessous. Pour information, il s’agit d’une réponse écho ICMP d’un serveur de Zeste de Savoir.
Offsets | Octet | 0 | 1 | 2 | 3 | ||||||||||||||||||||||||||||
Octet | Bit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
0 | 0 | IP v. 4 | IHL 5 | DSCP : 0 | ECN 0 | Longueur totale : 60 | |||||||||||||||||||||||||||
4 | 32 | Identification : 3580210 (8bda16) | Flags 0 | Fragment offset : 0 | |||||||||||||||||||||||||||||
8 | 64 | Time To Live : 52 | Protocole ICMP (1) | Header checksum | |||||||||||||||||||||||||||||
12 | 96 | Adresse IP source : 92.243.7.44 | |||||||||||||||||||||||||||||||
16 | 128 | Adresse IP destination : 192.168.1.10 | |||||||||||||||||||||||||||||||
Nous n’indiquons pas quelle est la checksum, car nous allons la calculer, comme si nous étions à la place du routeur qui a transmis ce paquet. Pour cela, on considère qu’elle vaut zéro.
Maintenant, retranscrivons ces valeurs en binaire et faisons abstraction des champs. Cela nous donne ceci :
Offsets | Octet | 0 | 1 | 2 | 3 | ||||||||||||||||||||||||||||
Octet | Bit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
4 | 32 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8 | 64 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
12 | 96 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
16 | 128 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
On découpe cela par blocs de 16 bits, qu’on additionne. Nous allons donc calculer la somme des nombres suivants :
- 0100010100000000
- 0000000000111100
- 1000101111011010
- 0000000000000000
- 0011010000000001
- 0000000000000000
- 0101110011110011
- 0000011100101100
- 1100000010101000
- 0000000100001010
Vous pouvez faire le calcul à la main pour vous entrainer. Sinon, une calculatrice binaire fait l’affaire.
Cela nous donne 10 0010 1010 1110 1000. Comme ce résultat s’écrit sur 18 bits et qu’il nous en faut 16, on va encore le découper, mais en commençant par la droite. On doit donc additionner les valeurs suivantes :
- 0010 1010 1110 1000
- 10
Vous trouverez aisément sans calculatrice que cela fait 0010 1010 1110 1010. Dernière chose, on inverse la valeur de chaque bit. Les 1 deviennent des 0, les 0 deviennent des 1. Cette opération s’appelle complément à 1. Nous obtenons ainsi comme valeur :
1101 0101 0001 0101
On peut aussi l’écrire en hexadécimal : D51516. Et voilà notre somme de contrôle de l’en-tête ! La preuve avec la capture du paquet d’origine, récupérée avec le logiciel Wireshark :
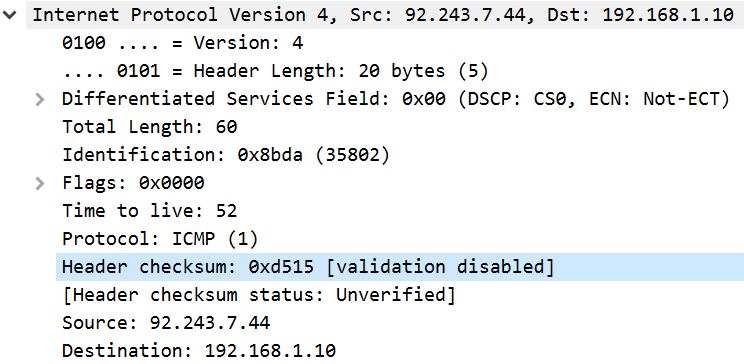
On peut voir sur cette image qu’IP n’a même pas pris la peine de vérifier cette somme de contrôle. Qu’à cela ne tienne, faisons-le nous-mêmes ! Pour cela, l’opération est exactement la même, on y inclut juste la checksum dans notre addition. Si tout se passe bien, le résultat final doit être égal à 0.
Nous avons déjà calculé la somme de tout le reste auparavant, cela donnait 10 0010 1010 1110 1000. Ajoutons-y la somme de contrôle transmise :
- 10 0010 1010 1110 1000
- + 1101 0101 0001 0101
Cela donne 10 1111 1111 1111 1101. Pareillement, on découpe 16 bits en partant de la droite, ce qui nous mène à la somme suivante :
- 1111 1111 1111 1101
- + 10
Ce qui fait 1111 1111 1111 1111. On termine en faisant un complément à 1, ce qui fait 0000 0000 0000 0000. On tombe bien sur 0, la somme de contrôle valide bien l’intégrité de l’en-tête !
Nous avons fait le tour de quelques méthodes de computation de somme de contrôle. Désormais, vous avez des notions de mathématiques qui vous serviront dans bien des domaines comme la cryptographie. L’aspect arithmétique des réseaux est peu attrayant et souvent occulté. Il est pourtant important que vous ayez quelques bases, c’est pourquoi cette annexe est là.